Parallel Transport on a Sphere

11 Mar 2024 · Comments

This post explains how parallel transport works on the surface of a sphere by solving the parallel transport equation and by highlighting some observations.

The parallel transport equation specifies how a vector can be parallel-transported:

\[\begin{equation} \frac{\partial V^{\alpha}}{\partial x^{\beta}} + \Gamma^{\alpha}_{\mu \beta} V^{\mu} = 0 \label{1} \tag{1} \end{equation}\]

In standard spherical coordinates ($\theta, \phi$), with $\theta$ being the colatitude, the angle measured from the z-axis where 0 is the North Pole ($0 \leq \theta \leq \pi$ rad), and $\phi$ being the angle from the x-axis in the xy-plane ($0 \leq \phi < 2\pi$ rad). If one is restricted to the surface of a sphere and by using the spherical metric after setting $r = 1$, one obtains the following metric:

\[\begin{equation} {\displaystyle ds^{2}=d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2}\,.} \label{2} \tag{2} \end{equation}\]

If one is interested in the parallel-transporting a vector along a constant latitude (ie a constant $\theta$), the components of a vector $\mathbf {V}$ change according to equation $\ref{1}$:

\[\begin{equation} \frac{\partial V^{\alpha}}{\partial \phi} = -\Gamma^{\alpha}_{\theta \phi} V^{\theta} -\Gamma^{\alpha}_{\phi \phi} V^{\phi} \label{3} \tag{3} \end{equation}\]

In order to do a parallel transport, one needs an initial vector. Using a local basis where

\[\mathbf{e}_{\theta} = \frac{\partial}{\partial \theta}, \quad \mathbf{e}_{\phi} = \frac{\partial}{\partial \phi}.\]

One can choose the initial vector $\mathbf {V}$ to be tangent to $\phi$ at the equator $(\theta = \frac{\pi}{2}, \phi = 0)$ with components $ V^\theta = 0, V^\phi = a$ where $a \in \mathbb{R}$ is a constant that indicates how many radians the vector stretches along the $\phi$ direction.

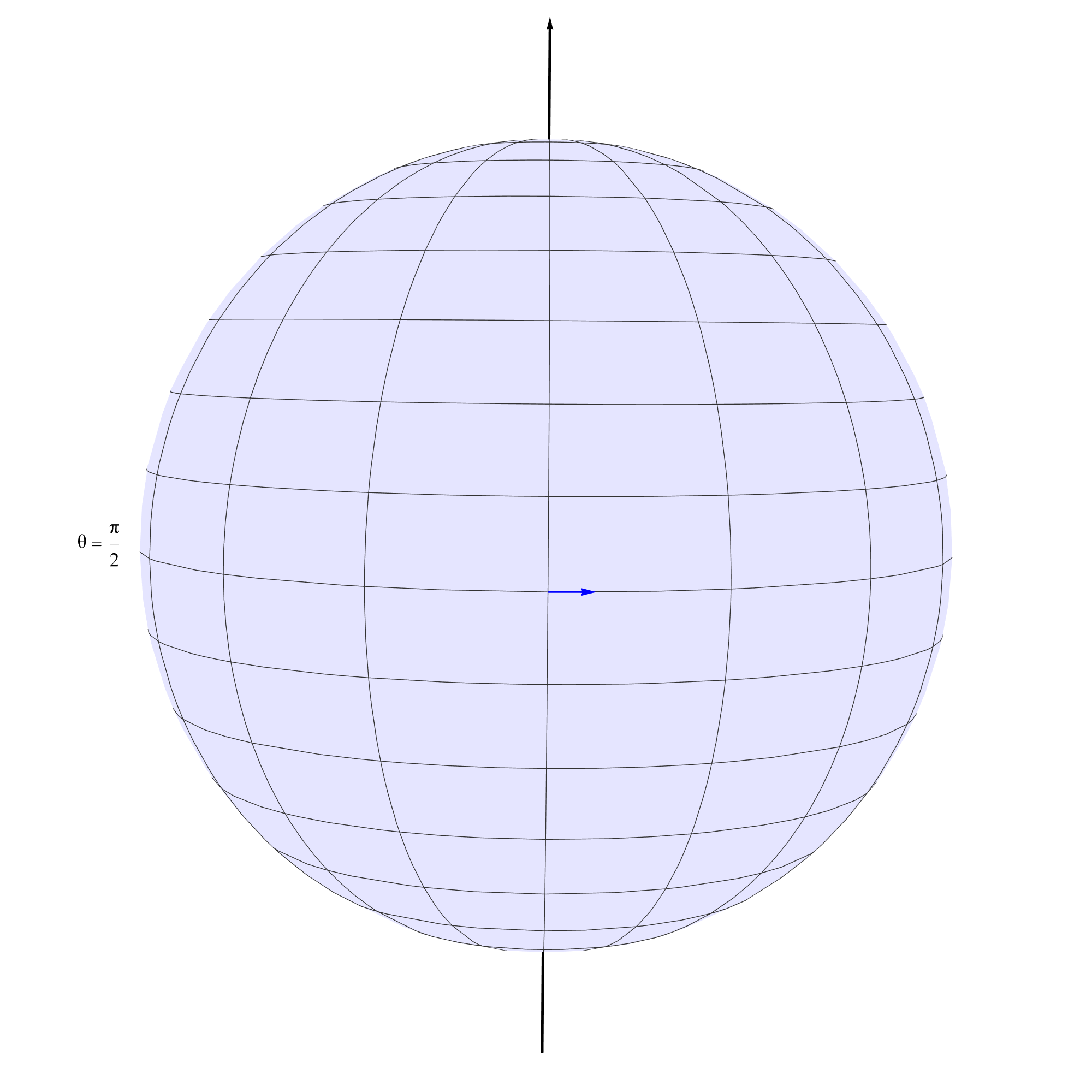
All that remains is solving equation $\ref{3}$. The Christoffel symbols can be computed from the metric ($\ref{2}$) as follows:

\[{\Gamma ^{\mu}_{\nu \sigma}={\frac {1}{2}}g^{\mu \alpha}\left({\frac {\partial g_{\alpha \nu}}{\partial x^{ \sigma}}}+{\frac {\partial g_{\alpha \sigma}}{\partial x^{\nu}}}-{\frac {\partial g_{\nu \sigma}}{\partial x^{\alpha}}}\right)}\]

One finds from equation $\ref{3}$ the following coupled partial differential equations:

\[\frac{\partial{V^\theta}}{\partial{\phi}} = \sin(\theta) \cos(\theta) V^\phi, \quad \frac{\partial{V^\phi}}{\partial{\phi}} = -cot(\theta) V^{\theta} .\]

The solutions to these equations must involve sines/cosines, using a computer algebra system one finds the following solutions:

\[V^\phi \left( \phi \right) = a \cos \left( \phi \, \cos(\theta) \right), \quad V^\theta \left( \phi \right) = a \sin (\theta) \, \sin \left( \phi \, \cos(\theta) \right).\]

These are functions in $\phi$ only; $\theta$ is constant in this case.

The following animation shows a sphere rotating along the z-axis with some vectors being parallel-transported for different values of $\theta$. The initial vectors are blue, and the parallel-transported vectors are green. As one can see, in general, after an amount of $\Delta \phi = 2\pi$ radians (ie one rotation), the vector does not coincide with the original one! This is due to the curvature of the sphere.

It can also be shown that parallel transport preserves the length of the vector. At the equator ($\theta = \frac{\pi}{2}$), the blue vector is not visible because the parallel-transported vector coincides exactly with the original one. This curve at the equator is called a great circle, which is a geodesic, and a gerodesic curve parallel-transports its own tangent vector, so it should be no surprise that both vectors coincide.

The angle $\alpha$ between the parallel-transported vector $\mathbf {V’}$ and the original vector $\mathbf {V}$ can be calculated with the aid of the metric using the following formula:

\[{\displaystyle \cos(\alpha )={\frac {g(\mathbf {V} ,\mathbf {V'} )}{\left\|\mathbf {V} \right\|\left\|\mathbf {V'} \right\|}}\,.}\] \[\begin{align*} \cos(\alpha ) =& \, \frac {g_{\mu \nu}V^\mu V'^\nu}{\sqrt{g_{\rho \sigma}V^\rho V^\sigma} \, \sqrt{g_{\rho \sigma}V'^\rho V'^\sigma}} \\ =& \, \cos(2\pi \, \cos (\theta)) \end{align*}\] \[\Leftrightarrow \alpha = \pm 2\pi \, \cos (\theta) + 2\pi n, \quad n \in \mathbb{Z}.\]

It is now evident that the angle $\alpha$ depends on $\theta$.

For example, taking $\theta = \frac{\pi}{2}$, one finds $\alpha = 0$. For $\theta = \frac{\pi}{3}$, one finds $\alpha = \pi$ which is the opposite direction of the initial vector.

Comments